64=65 บ้านเธอซิ่

อ.ดร.วัชรินทร์ วิชิรมาลา

ในช่วงที่ผ่านมามีการระบาดในอินเตอร์เน็ตของภาพชุดเป็นลำดับแสดงสิ่งประหลาดที่แสดงว่า 64=65 ดังแสดงข้างล่างนี้

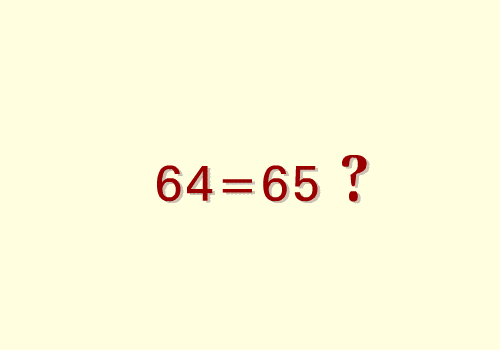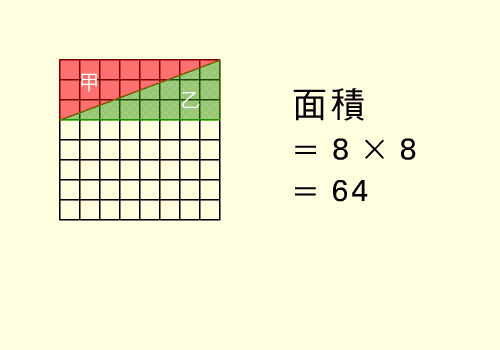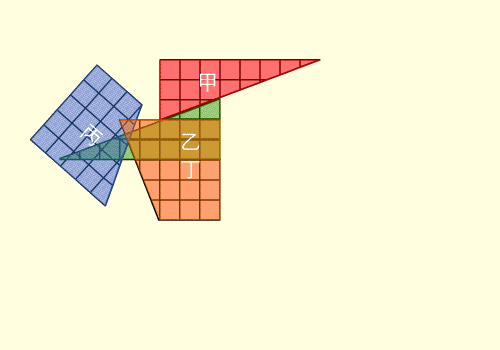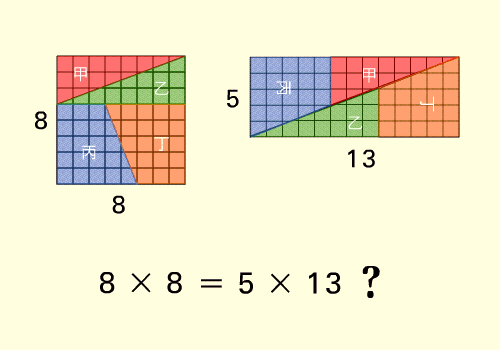
หัวข้อของอีเมลที่ส่งมาหาผมคือ”วงการคณิตศาสตร์สั่นสะเทือน!!”

ก่อนดูผมก็คิดย้อนไปถึงประสบการณ์ของตัวเองเมื่อเกือบ 20 ปีก่อน ที่ผมได้ไปพิพิธภัณฑ์วิทยาศาสตร์ที่ติดกับท้องฟ้าจำลองและพบกับการตัดแบ่งสี่เหลี่ยมอันหนึ่งแล้วประกอบเข้ากันใหม่ให้มีพื้นที่เพิ่มขึ้น! ภาพแสดงการตัดต่อนั้นทำเอาผมอึ้งอยู่นานหลายนาทีกว่าจะรู้ว่าถูกหลอกอย่างไร

กลับมาเรื่องปัจจุบัน

หลังจากเปิดดูก็พบว่ามันคือการหลอกตาแบบเดียวกันเป๊ะเลย ที่นำสี่เหลี่ยมจตุรัสขนาด 8x8 มาตัดแล้วต่อกันใหม่เป็นสี่เหลี่ยมผืนผ้าขนาด 5x13 ทำให้พื้นที่เพิ่มขึ้นจาก 64 มาเป็น 65

แน่นอนครับว่า 64 มันไม่เท่ากับ 65 แต่ทำไมมันดูไม่ออกเลยว่าปัญหาอยู่ที่ไหน

จะเห็นว่าถ้าเราพิจารณาการแบ่งรูปแรกประกอบกับขอบของรูปที่สอง จะพบว่าไม่มีอะไรผิดปกติ ดังนั้นปัญหาน่าจะอยู่ในรอยเฉียงของรูปที่สอง สิ่งที่ผมลองเมื่อ 20 ปีที่แล้วยังคงเป็นการวิเคราะห์ปัญหาแบบตรงประเด็น กล่าวคือความชันของเส้นทแยงมุมมันไม่เท่ากันตลอด หรือพูดง่าย ๆ ว่ามันไม่ใช่เส้นตรงอย่างที่เราเห็นนั่นเอง

ก่อนอื่นเราต้องแนะนำก่อนว่าความชันคืออะไร ทุกคนรู้ดีอยู่แล้วว่าเส้นสองเส้นชันเท่ากันหมายความว่าอะไร เส้นนี้ชันกว่าเส้นนั้นแปลว่าอะไร แต่ในทางคณิตศาสตร์เรานิยามความชันไว้อย่างรัดกุมไร้ความคลุมเครือเพื่อป้องกันการถกเถียง ก่อนอื่นเราต้องพูดถึงกรอบอ้างอิงก่อนว่าเราจะมองจากทางด้านไหน หรือว่ากันง่าย ๆ คืออะไรเป็นของบนล่างและซ้ายขวาของภาพ ไม่งั้นนกแก้วกับค้างคาวคงเถียงจนฆ่ากันตายแน่ ในที่นี้หากเราตกลงว่าเรามองภาพตามทิศการอ่านหนังสือแบบปกติที่คนปกติไม่เพี้ยนเขาทำกัน ก็จะได้ว่าความชันของเส้นตรงคือสัดส่วนความสูงส่วนฐาน เราต้องเริ่มจากเส้นเฉียงจากบนขวาลงซ้ายล่าง

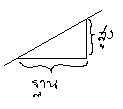
หากเส้นเฉียงไปอีกทางจากบนซ้ายลงขวาล่างก็จะได้ความชันติดลบ

ด้วยข้อตกลงนี้ เส้นนอนก็จะมีความชันเป็นศูนย์ และเส้นตั้งแนวดิ่งไม่มีความชัน หรือบางคนก็บอกว่าความชันเป็นอนันต์ เมื่อ

เราใช้ระบบพิกัดฉากที่มีแกน X และแกน Y เข้ามาช่วย การหาความชันก็จะง่ายมาก

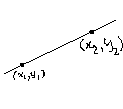
เพียงแต่หาจุดสองจุดบนเส้นนี้ ขอแทรกหน่อยว่าผมรำคาญเหลือเกินกับคำฟุ่มเฟือยที่ว่า “เส้นตรงสองเส้นที่ไม่ใช่เส้นเดียวกัน” หรือ “จุดสองจุดที่ไม่ใช่จุดเดียวกัน” จะบอกไปทำไม ถ้ามันจุดเดียวกันมันก็มีแค่จุดเดียวนะซิ่ ไม่ใช่สองจุด เพราะฉะนั้นถ้าบอกว่าสองจุด มันก็ไม่น่าจะต้องบอกว่า “ที่ไม่ใช่จุดเดียวกัน” ความชันของเส้นนี้ก็จะเป็น หรือ สูตรนี้ก็จะชี้ให้เห็นว่าหากเส้นเฉียงจากบนซ้ายลงขวาล่างก็จะมีความชันเป็นค่าลบ และกรณีที่เป็นเส้นตั้งแนวดิ่ง ตัวหารก็จะเป็นศูนย์ทำให้ความชันไม่นิยาม หรือบางพวกอาจเรียกเล่น ๆ อย่างไม่เป็นทางการว่าความชันเป็นอนันต์หรืออินฟินิตหรืออินฟินิตี้

ทีนี้เราก็พร้อมที่จะพิจารณาความชันของเส้นปัญหาที่เราสงสัย

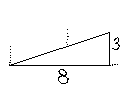
ในส่วนแรก ความชันเป็น 3/8 = 0.375

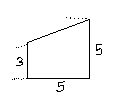
ในส่วนที่สอง ความชันเป็น 2/5 = 0.4

จะเห็นได้ว่าความชันของสองท่อนมันใกล้กันมาก ทำให้เราเข้าใจผิดว่ามันเป็นเส้นตรงเดียวกัน

อ้าว! แล้วทำไมมันดูเนียนจัง?

ปัญหาอีกกันคือความหนาของเส้นครับ ความหนาของเส้นทำให้เส้นที่เป็นคนละเส้นมันแยกจากกันไม่ออกด้วยตา หากเราใช้เส้นที่ผอมกว่าจะเห็นได้ว่ามีรอยแยกตรงกลางรูปที่สอง รอยแยกนี้มีพื้นที่หนึ่งหน่วยนั่นเอง

ทีนี้เราคงซาบซึ้งแล้วนะครับว่าทำไมนักคณิตศาสตร์เขาบัญญัติไว้ว่า “จุดคือตำแหน่งที่ไม่มีขนาด” และ “เส้นคือแนวที่ไม่มีความหนา” ไม่งั้นก็คงจะเจอปัญหามากมายเถียงกันไม่จบไม่สิ้น สุดท้ายนี้ขอทิ้งท้ายด้วยคำถามกวนบาทาอันหนึ่ง

“จุดไม่มีขนาด และเส้นประกอบด้วยจุดที่ไม่มีความยาว เอแล้วทำไมเส้นมีความยาวหว่า?”